June 2017 Issue
Research Highlights
Inference of Bayesian networks made fast and easy using an extended depth-first search algorithm
A Bayesian network is a directed acyclic graph (DAG) or a probabilistic graphical model used by statisticians. Vertices of this model represent different variables. Any connections between variables indicate a conditional dependency and a lack of connections implies a lack of it.
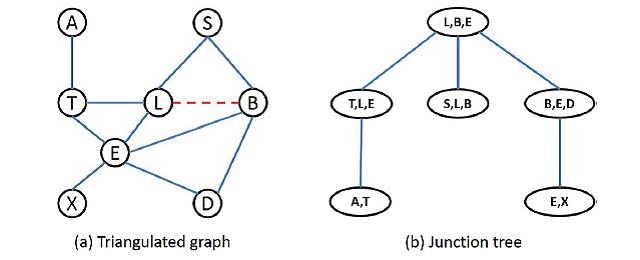
Traditionally, Bayesian networks are used for modelling and inference of large amounts of information using algorithms. One such common algorithm is the junction tree algorithm that uses the method of triangulation: The DAG is simplified into triangles, based on the connections (regardless of direction) and subsequently cliques making up each triangle act as junctions or "nodes" of a hierarchical tree. Ottosen and Vomlel first proposed the depth-first search (DFS) algorithm based on this principle. The DFS algorithm was based on two components: depth-first search and dynamic clique maintenance to scan and eliminate nodes and identify new cliques, respectively. However this method is time-consuming and leads to problems such as finding the same clique twice.
Here, Chao Li and Maomi Ueno at the University of Electro-Communications in Tokyo have further refined this algorithm and created a new extended depth first algorithm (EDFS). Based on their algorithm, only cliques with new edges introduced are selected, thus making clique selection very specific. Their second improvement to the algorithm is "pivot clique pruning". This is a sophisticated method of eliminating orders or variables from the network, which greatly reduces the size of the search tree.
To validate the EDFS algorithm, the researchers randomly compared networks from a well-known database with the DFS algorithm. They found that the total running times and time for depth first search and dynamic clique maintenance were less compared to the DFS algorithm.
"The new EDFS algorithm improves the state-of-the-art Ottosen and Vomlel (DFS) algorithm in two orthogonal directions: (1) reduction of the overhead cost, and (2) reduction of the size of the search space," conclude the authors. Time-efficient analysis of Bayesian networks can lead to quick deduction of vast amounts of data.
Reference
Chao Li and Maomi Ueno. "An extended depth-first search algorithm for optimal triangulation of Bayesian networks." International Journal of Approximate Reasoning, Published online (30 September 2016); doi: 10.1016/j.ijar.2016.09.012
http://dx.doi.org/10.1016/j.ijar.2016.09.012